Modell drehen: Maustaste 1
Modell zoomen: Mausrad
Modell verschieben: Maustaste 2
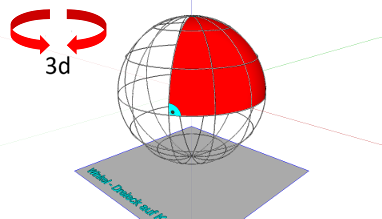
Körper mit gekrümmten Flächen
Kugel, Dreieck
Winkel auf gekrümmten Flächen - Kugel
In diesem Modell kann man am Beispiel der Kugeloberfläche plastisch sehen, dass es Dreiecke gibt, deren Innenwinkelsumme ungleich 180° ist - wie dies ja für ebene Dreiecke gilt.
Für die Kugeloberfläche ist die Winkelsumme größer als 180° - eine Folge der Krümmung der Kugeloberfläche.
Das hängt damit zusammen, dass ihre Gaußsche Krümmung ungleich 0 ist und - anschaulich gesprochen - damit, dass sich die Kugeloberfläche nicht verzerrungsfrei in die Ebene abwickeln lässt.
Für den Zylindermantel und den Kegelmantel ist die Innenwinkelsumme von Dreiecken gleich 180°, weil sie sich - anschaulich gesprochen - verzerrungsfrei in die Ebene abwickeln lassen und ihre Gaußsche Krümmung = 0 ist.
Übrigens: Es gibt auch Flächen, bei denen die Innenwinkelsumme kleiner als 180° ist.