3D-Mathematik - 3D-Modell

Geometrie
Körper mit gekrümmten Flächen
Kegel
Volumen - Berechnung, Formel

Diese Serie von Modellen zeigt geometrische Körper, die durch gekrümmte Flächen begrenzt sind und behandelt ihre Berechnung. Gekrümmte Flächen folgen weiter unten.

Dieses und die folgenden Modelle behandeln die Formeln, mit denen man das Volumen und die Oberfläche eines senkrechten Kreiskegels ermitteln kann. Hier wird gezeigt, wie man in zwei Schritten das Volumen berechnen kann.

Symbole:
V = Volumen, G = Grundfläche, m = Mittelpunkt, r = Radius der Grundfläche, h = Höhe, Pi = Kreiszahl 3,14 (genauer = 3,1416)

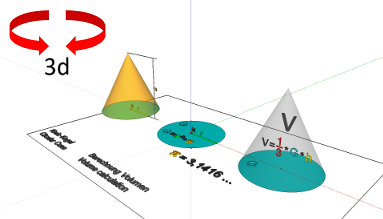
Linkes Modell: Gegeben sind zwei Größen - der Radius r der Grundfläche und die Höhe h des Kegels. Mehr nicht - und das reicht.

Mittleres Modell - Schritt 1:
Berechne die Grundfläche G (die Fläche eines Kreises!) - Grundfläche G = Radius r mal Radius r mal Pi (G=r*r*Pi=r²*Pi).

Rechtes Modell - Schritt 2:
Berechne das Volumen V = 1/3 mal Grundfläche G mal Höhe h (V = 1/3 *G*h).

Beim Zylinder gilt die einfache Formel für das Volumen V = Grundfläche G mal Höhe h (V=G*h).
Beim Kegel tritt nun noch ein Faktor 1/3 auf (V = 1/3 *G*h). Was dieser Faktor bewirkt und wie man zu diesem Faktor kommt zeigen die beiden folgenden Modelle.