3D-Mathematik - 3D-Modell

Geometrie
Körper mit gekrümmten Flächen
Kegel
Volumen - Formel - Scheibenmethode (Cavalieri)

Diese Serie von Modellen zeigt geometrische Körper, die durch gekrümmte Flächen begrenzt sind und behandelt ihre Berechnung. Gekrümmte Flächen folgen weiter unten.

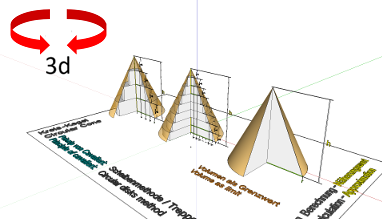
In diesen Modellen zeigen wir einen der Ansätze, über den man schließlich zu dem Faktor 1/3 in der Volumenformel des Kegels gelangt - die sogenannte Scheibenmethode nach Cavalieri; anstatt von Scheiben spricht man auch von Treppenkörpern (um weitere Modelle zu diesem Ansatz zu sehen in der Galerie im ‚Freitext‘-Feld ‚Cavalieri‘ eingeben).

Links: Hier wird die Höhe des Kegels in vier gleich große Teile geteilt, sodass dem Kegel drei Scheiben in der Form von Zylindern einbeschrieben werden können, deren Volumen sehr leicht berechnet und anschließend aufaddiert werden kann. Diese grobe Teilung führt zu einer recht ungenauen Abschätzung des Kegelvolumens.

Mitte: Hier ist die Teilung der Kegelhöhe verfeinert und die Zahl der Scheiben bzw. Treppenstufen erhöht. Die Berechnung erfolgt wie eben und die Abschätzung des Volumens wird schon deutlich besser.

Verfeinert man diese Teilung weiter, gelangt man schließlich zu dem Faktor 1/3 - einem Grenzwert. Die mathematische Herleitung ist anspruchsvoll, aber auch nachvollziehbar!

Wir haben hier ‚einbeschriebene‘ Scheiben (Treppenkörper) verwendet, die innerhalb der Pyramide liegen. Man kann aber auch ‚umbeschreibende‘ Scheiben (bzw. Treppenkörper) verwenden - mit dem gleichen Grenzwert.