3D-Mathematik - 3D-Modell

Geometrie
Körper mit gekrümmten Flächen
Kugel, Kugelfläche
Volumen - Berechnung, Formel (Archimedes)

Diese Serie von Modellen zeigt geometrische Körper, die durch gekrümmte Flächen begrenzt sind und behandelt ihre Berechnung. Gekrümmte Flächen folgen weiter unten.

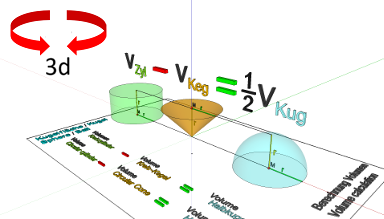
Dieses Modell lehnt sich an die sog. ‚Archimedische Herleitung‘ an, eine unglaublich einfache Methode der Volumenberechnung der Kugel - die übrigens in der Konsequenz zu jenem Faktor 4/3 in der Volumenformel führt.

Symbole:
V … = Volumen des Objekts, M = Mittelpunkt, r = Radius und Höhe

Links und in der Mitte sind ein Zylinder und ein Kegel zu sehen. Beide haben ganz bestimmte Maße – ihr Radius und ihre Höhe sind gleich r! Die Volumenberechnung von Zylinder und Kegel haben wir in den vorherigen Modellen behandelt.

Nun sehen wir, dass das Volumen des Zylinders minus das Volumen des Kegels das Volumen der Halbkugel mit Radius r ergibt. Wirklich? Ja! Ich glaub es nicht! Dann schau mal in das nächste Modell und in die ‚Quellen‘!